The intrinsic value of a fair bet is one in which the cost of the bet is identical to the expected after-tax, net cash payoff. For example, if you had a lottery ticket that promised a 7% chance to win $100, a fair bet would be $7.00. If you could buy the bet for significantly less than $7.00, it is a “good” bet. You may still lose, because the chances of winning remain small, but you are not being cheated on the price that is being paid for the potential win, unlike, say, a slot machine where a $1.00 spin should really only be valued at between 80¢ and 95¢ depending on the particular machine (meaning you will lose all of your money if you play long enough).
Likewise, if you had an elementary school raffle ticket that gave you a 2% chance to win a $50,000 car, the “fair” price is $1,000. If you could buy these tickets for $200 each, you would want to acquire every single ticket for a total cost of $10,000 and a guaranteed profit of $40,000, even if you went on to sell the car. It would be a pure arbitrage situation, though your neighbors might think you were a jerk.
Intrade and Basic Probability Theory
To provide a real world example, let’s look at Intrade. Intrade is a speculation market where traders can get together and wager on the outcomes of real world events. Someone who thinks an event will not happen ‘sells’ shares, while someone who thinks and event will happen ‘buys’ shares. Their bidding activity sets the price. At the end of the event, shares settle at one of two prices, either $0, if the event did not occur, or $10.00 if the event did occur. The Intrade market takes a base fee of roughly $5 per month to participate on its platform.
For those who have an interest in probability theory and don’t mind playing with a little side money, it can be a very fun thing. For those with a gambling or adrenaline addiction, it is a nightmare waiting to happen. I hate gambling, both intellectually and emotionally, but when specific probabilities become highly favorable, I am not opposed to occasionally taking a position with some of my discretionary, personal cash.
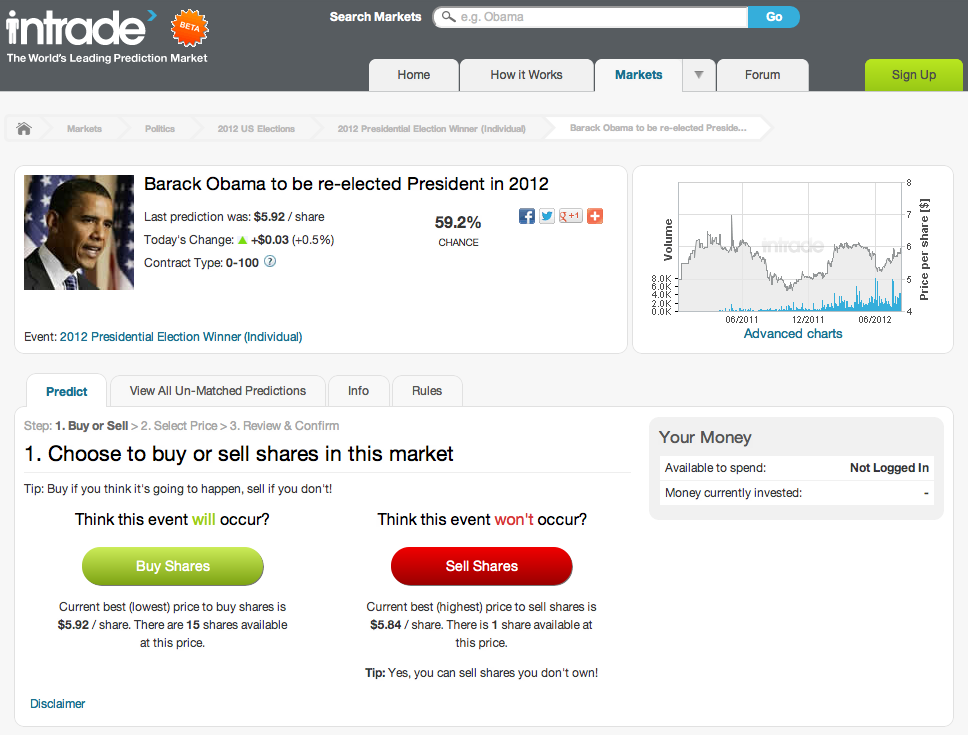
[mainbodyad]Take, for example, the 2012 election for the President of the United States. Right now, if you believe that Barack Obama will win the presidency, you can buy shares for $5.90. As of this moment, there are only 21 shares available, so that is only $123.90. If you think he will lose the presidency, you can sell shares at $5.83, and there are 277 shares available, or $1,614.91. Based upon the total volume of shares traded to date, the markets are setting a 59.0% chance of re-election for Obama. (There are actually far more unmatched shares if you are willing to move up or down in price on either respective side of the transaction but we are going to keep it simple for now to illustrate basic probability.)
If Obama wins, the shares settle at $10.00. If he loses, they settle at $0.00. Someone who bought shares wants the $10.00 settle price, while someone who sold shares wants the $0.00 settle price.
However, Nate Silver, one of the best statisticians alive who boasts one of the best records on predicting electoral outcomes, calculates a 71.6% probability that Barack Obama will win the election in early November based upon all available data as of this afternoon. That would imply that the “fair” price of one of the shares, were you a buyer, would be $7.16, adjusted for the total fees you have to pay as a member of the site. The current price of $5.90 represents a $1.26 discount to intrinsic value, or 17.6%.

If Nate Silver’s electoral forecasts are correct, it means there is a mismatch in market price and intrinsic value price on the Intrade exchange.
On the other hand, the intrinsic value for selling shares short is different because the maximum payoff itself is equal to the current market price. That is, if the event does not happen, you get to keep the entire current market price because the shares settle at $0. This leads to situation that, when the odds are not in your favor, there is no price at which you should take a bet on this side of the table.
For example, right now, if you sold shares of the election short, you would get to keep the entire $5.83 payoff. Taking your maximum payoff and multiplying by the odds of winning (in this case, 28.4%, or .284), the intrinsic value of the sell side should be $1.66 per share, not the $5.83 the market currently demands. However, if the shares were at $1.66, you would perform the same calculation and find that the intrinsic value is now only $0.47 per share. This would continue until reaching $0. Given the pricing mechanics of this particular market, you cannot rely on the simplistic “fair bet” price to calculate what would amount to a stock option on the election. This leads to the conclusion that the sell side position is overvalued based upon current analysis.
Thus, a trader of the shares at this price is getting more value than he is paying for in the price if he is a buyer, and getting less value than he is paying for if he is a seller. On a coldly probabilistic basis, one is a good bet and one is a bad bet. That doesn’t mean you should take either position because this is not investing, it is gambling. The chances of loss are very real. I’m simply using it as a teaching tool.
The Human Equation Is What Makes Human Probabilistic Outcomes So Interesting
The thing that makes payoffs interesting is the human equation. What happens if the delegates to the Republican convention, look at the figures and realize Mitt Romney is running at an almost 3-1 disadvantage on a county-by-county analysis, and decide to throw the rule book out to award their votes to someone completely unexpected? With enough arm twisting, it is entirely possible someone like Chris Christie or Michael Bloomberg could be the nominee by the time the convention were concluded. In such a case, the probabilities would shift wildly (I’m guessing, not in favor of President Obama, especially in several swing states). The shares could still expire worthless at $0.00 each. That is the luck portion of mathematics.
In any event, this is not something people should be doing with their money. I have no wagers of any sort at the present time, nor I have any plans to enter into one, on the Presidential election. I thought it was an interesting way to teach complete beginners about “good” and “bad” bets relative to the fair bet price.
[mainbodyad]